1.STAGE 4:企業価値の算定
今回の連載第15回では、エンタプライズDCF法の実務の仕上げであるSTAGE 4を説明します。STAGE 4では、これまでの各ステージで得られた数値と、以下に説明する継続価値の現在価値を合算して、最終的に企業価値を算定します。
連載
第13回から
14回で説明したSTAGE 2では、将来の一定の「詳細予測期間」(モスフードサービスの例では7年間)について業績を予測し、そこから、DCF法により企業価値を求める場合に必要な将来フリー・キャッシュフローを予測しました。この詳細予測期間以降の期間を「存続期間」と呼び、存続期間に発生すると予測されるフリー・キャッシュフローの現在価値の総和、すなわち「継続価値」は、単純な公式に基づいて算出されることも説明しました。今回は、まずこの継続価値について解説しましょう。
継続価値を算定するために、実務上使われている代表的な公式には、フリー・キャッシュフロー恒久成長式とバリュー・ドラーバー式の2種類あります。これらの公式で求めた継続価値を現在価値に割り引いたものを、予測期間におけ るフリー・キャッシュフローの現在価値と合算すると事業価値が求められ、その後非事業用資産を加算することで、企業価値が求められます。
本章では、この過程をさらに細かく、以下のような4つのステップに分けて説明します。
STEP 1:継続価値算定の公式の選択
STEP 2:継続価値の公式における変数(パラメータ)の設定と継続価値の算定
STEP 3:事業価値の算定
STEP 4:企業価値(および株主資本価値)の算定
以下、これらの各ステップにおいて、どのような点に留意して作業をするかを説明したうえで、具体的なイメージを持ってもらうために、モスフードサービスの企業価値計算の実例を用いて、実際の手順を確認していきましょう。
STEP 1:継続価値算定の公式の選択
継続価値算定の公式として、筆者が推奨するのは、バリュー・ドライバーを明示的に含んだ、以下のようなバリュー・ドライバー式です。
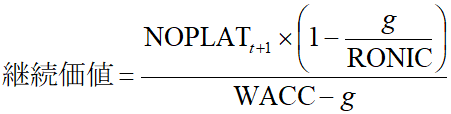
ただし、
NOPLATt+1: フリー・キャッシュフロー予測期間最終年の翌年の標準化したNOPLAT
g:NOPLATの長期(恒久)成長率
RONIC:新規投資(純増分)に対する投下資産利益率
WACC:税引後加重平均資本コスト(STAGE 3で算出)
バリュー・ドライバー式においては、成長率、既存の投下資産のROIC、新規投資の投下資産利益率(RONIC)、税引後加重平均資本コスト(WACC)といった、企業価値の根源となるバリュー・ドライバーが変数として明示的に含まれています。この式は、3つの前提の下に導かれます。
1. 企業は存続期間において、一定の利益率を獲得し、資本回転率、既存の投下資産の投下資産利益率(ROIC)は一定。
2. 企業の売上と、みなし税引後営業利益(NOPLAT)は、一定の割合で増加。NOPLATの一定割合は、毎年純増分の新規投資として既存の投資に上乗せ。
3. すべての新規投資(純増分)の投下資産利益率(RONIC)は、一定。(注)
もう1つの継続価値算定の公式は、フリー・キャッシュフロー恒久成長式です。これは、予測期間最終年の標準化したフリー・キャッシュフローが、予測期間以降に一定の成長率で成長することを前提に、予測期間最終年の翌年のフリー・キャッシュフローから直接算定するモデルで、実務上も多用されています。フリー・キャッシュフロー恒久成長式(以下、FCF式と呼びます)は、以下のようになっています。
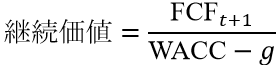
ただし、
FCFt+1: フリー・キャッシュフロー予測期間最終年の翌年の標準化したFCF
g:FCFの長期(恒久)成長率
WACC: 税引後加重平均資本コスト
実は、バリュー・ドライバー式は、FCF式における予測期間最終年の翌年のフリー・キャッシュフロー(FCF
t+1)に関して、予測最終期のNOPLATの一部を、永続的に一定の再投資比率で再投資(追加投資)し、その再投資が永続的にRONICの利益率で追加的にNOPLATを生み出してNOPLATが成長する、という前提で、フリー・キャッシュフローを書き直したものと考えることができます。具体的には、まず予測最終年の翌年(t+1年後)以降のNOPLATの再投資比率をiとすると、フリー・キャッシュフローは、NOPLATのうち、再投資されなかった結果として、投資家に提供される部分なので、以下のように書けます。
FCF=NOPLAT×(1-i)
また、再投資分は、RONICで運用されてNOPLATの成長をもたらすので、成長率との関係でいうと、g=i×RONIC となります。したがって、
g RONIC と計算され、
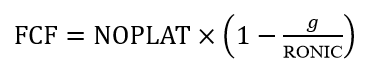
と書けます。
こうしてFCF式の分子の部分に、
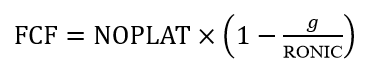
という関係式を代入することによって、バリュー・ドライバー式が導かれることがわかります。バリュー・ドライバー式においては、継続価値計算の成長率(g)の源泉が、投下資産への追加的な投資(投資の上積み)にあることが明示的に示されている点が優れているといえます。
企業価値評価においては、長期成長率の変化が継続価値や企業価値にどのような影響を与えるかをシミュレーションすることがありますが、この際、FCF式を用いて単純に計算すると、成長率に応じて必要となる再投資額は異なり、結果としてフリー・キャッシュフローも異なるという事実を無視していることになります。この点において、バリュー・ドライバー式は、FCF式よりも、より客観的計算を可能にするように思われます。
FCF式、バリュー・ドライバー式、どちらの公式を用いるにしても、公式の分子に入力するNOPLATやFCFは、予測最終年の翌年((t+1)年)のものを用います。ここで注意すべきは、これらの公式を用いて計算された値は、予測最終年(t年)における現在価値を示すということです。したがって、これらの公式の計算結果を現在価値に直すためには、さらに税引後WACCを用いてt年分割り引かなければなりません。すなわち、

これ以外にも、継続価値を計算する方法として、各種マルチプル法(EV/EBITDA、EV/EBITマルチプル等)がしばしば併用されます。この手法は、予測最終年度において企業を他社に売却することを前提に、その売却金額を一定のマルチプル(乗数)で推定して一括計上する考え方で、バリュー・ドライバー式等の公式で求めた継続価値の水準の妥当性を確認するために用いられることが多いようです。なお、この乗数を求めるときには、評価時点での乗数と、予測期間最終期における乗数が一致する保証はないことに注意しましょう。特に、評価時点で売上や利益が高成長期にある企業の場合、乗数は評価時点をピークに低下していくのが通常ですので、その点を勘案せずにマルチプル法を適用すると、継続価値を過大評価する可能性が高いので、十分に注意しましょう。なお、マルチプル法については、次回連載の最終回で、再度取り上げます。
STEP 2:継続価値の公式における変数(パラメータ)の設定と継続価値の算定
継続価値算定の公式を利用する際に、決定しなければならないパラメータ(変数)として、バリュー・ドライバー式の場合、NOPLAT、RONIC、NOPLATの成長率、税引後WACCがあります。これらのパラメータは、将来予測を立てる作業との整合性を意識しつつ決定します。
① NOPLAT
ベースとなるNOPLATの水準については、標準化という作業を行なった後のNOPLATを使います。標準化とは、予測期間以降に長期的に維持可能なフリー・キャッシュフローの実態を見極めることです。注意すべき点として、一般に予測期間の成長率よりも、長期(恒久)成長率は低い成長率を用いる場合が多いため、継続期間における新規投資、および、その結果としての減価償却費は、予測期間内のものよりも少なくなることが予想され、それを反映したNOPLAT予測を立てる必要があります。また、シリコン・サイクルで知られる半導体製造業のように、売上に周期性のある企業においては、継続価値計算に用いるNOPLATは、売上のビジネス・サイクルのピークとボトムの中間点となるように標準化する必要があります。
② RONIC(新規投資分のROIC)
予想期間後の新規投資分のROIC(RONIC)を求める際には、予想期間内の各年度におけるROICやRONICを参考に、予測期間終了後、未来永劫を展望して平均的に達成可能なRONICの水準を決定します。なお、RONIC<税引後WACCの場合、経営者はそのような新規投資をしないはずなので、RONIC≧税引後WACCの関係が成り立つはずです。超長期的に見れば、企業の新規投資機会の収益率は、投資リスクに対して投資家が期待した収益率並み、すなわち、RONIC=税引後WACCとなる可能性が高いですが、高いブランド力を持つ高級品メーカーや、不断の新薬開発により高収益を維持する製薬業のように、長期的に税引後WACCを超えるRONICを維持しているケースもあります。いずれにせよ、長期的にRONIC>税引後WACCを仮定するのであれば、他社に比して競争力を維持できると考える理由が必要です。
③ NOPLATの長期(恒久)成長率
長期成長率については、経済全体の長期名目成長率予測(日本企業でその営業基盤が日本国内の場合は、日本経済の長期名目成長率予測)を上回る数字を用いることは非現実的です。なぜならば、そのような状況が超長期にわたって継続すると、その企業はいつの日か、経済全体の合計を上回る企業規模を持つようになってしまうからです。また前述のように、バリュー・ドライバー式は、予測最終期のNOPLATの一部を、永続的に一定の再投資比率で再投資する、という前提で予測するモデルですので、成長率とRONICから逆算される再投資比率(i)を見て、評価対象企業の長期的イメージとの間で整合性があるかどうか、確認する必要があります。
以上の点に留意して、継続価値を計算する公式と、それに適用する諸変数が…
■鈴木 一功(すずき かずのり)早稲田大学大学院経営管理研究科(早稲田大学ビジネススクール)教授
東京大学法学部卒業後、富士銀行入社。INSEAD(欧州経営大学院)MBA(経営学修士)、ロンドン大学(London Business School)金融経済学博士(Ph.D. in Finance)。M&A部門チーフアナリストとして、企業価値評価モデル開発等を担当の後、2001年から中央大学大学院国際会計研究科教授。2012年4月より現職。証券アナリストジャーナル編集委員、みずほ銀行コーポレート・アドバイザリー部のバリュエーション・アドバイザー。主な著書として『企業価値評価(入門編)』、『企業価値評価(実践編)』、『MBAゲーム理論』(いずれもダイヤモンド社)、他にコーポレート・ファイナンス、M&Aに関する論文多数。
※詳しい経歴は
こちら